Comparison of Forms - a Possible Criterion
in Geometrical Deformation Analysis

Frank Neitzel and Svetozar Petrovic

Institute of Geodesy and Geoinformation Technique, Berlin University of Technology

In geometrical deformation analysis a set of points is compared in two (or more) epochs. In case that the geodetic datum is unknown some kind of transformation (e.g. Helmert- transformation) has to be done. But the residuals after such a transformation are not easy to interpret because they are composed of three parts:

residual after transformation = real deformation + transformation defect + random error

The only solution is to classify the points into groups of stable and instable points. In standard solutions this decision is done using metric criteria. An example (taken from Reinking, 1994) is given which shows that one of the standard solutions (localization with "S-transformation") does not lead to a correct result.

As an alternative to this, our proposal is to use a comparison of forms which can be described by the correlation coefficient (squared) r 2, for instance in the following form:

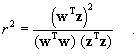
r2.gif

The vectors zT and wT contain the coordinates of points in epoch I resp. II.

After a maximum correlation adjustment (MCA) and the computation of the correlation coefficient between the sets of coordinates associated with the two epochs as a criterion for the similarity of forms, we are able to find the stable and instable points even in cases where solutions based on metric criteria failed.

References:
NEITZEL, F. (1999): Ausgleichung nach maximaler Korrelation in der geometrischen Deformationsanalyse. Diplomarbeit, TU Berlin, Institut für Geodäsie und Geoinformationstechnik
PETROVIC, S. (1991): Geometry of the Correlation Coefficient and its Application in Geodesy. Mitteilungen der geodätischen Institute der Technischen Universität Graz, Folge 71
REINKING, J. (1994): Geodätische Analyse inhomogener Deformationen mit nichtlinearen Transformationsfunktionen. DGK, Reihe C, Nr. 413, München

Back