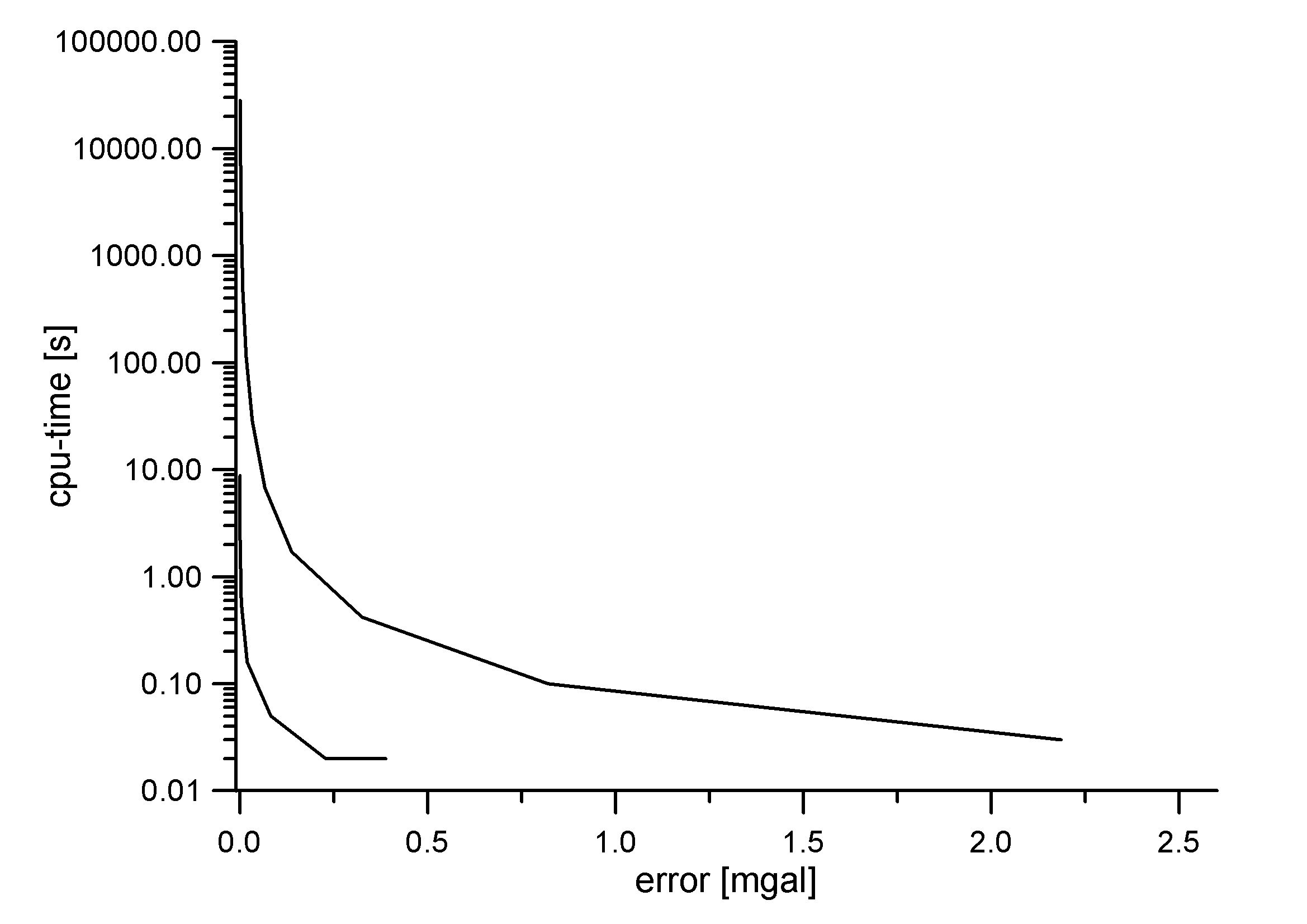
CPU-time needed for the same accuracy of the computation of the amount of the gravity vector
for the regular prisms method (upper curve) and the polyhedra method (lower curve)
Svetozar Petrovic and Piotr Skiba
Institute of Geodesy and Geoinformation Technique, Berlin University of Technology
One of the possibilities to compute gravitational effects is to use homogeneous elementary bodies such as rectangular prisms or general polyhedra. In last decades several papers appeared dedicated to polyhedra; however almost exclusively in geophysical publications. Obviously, geodesists still prefer rectangular prisms which imply the use of grid data and a planar model.
In order to compare the efficiency of both approaches, a grid data from the West Alps and the planar model were used. It came out that the rectangular prisms require much more CPU-time than the polyhedra in order to achieve the same accuracy. A typical relation is visible in the enclosed figure.

References:
Petrovic S (1996)
Determination of the potential of homogeneous
polyhedral bodies using line integrals: Journal of Geodesy, 71,
44-52.
Skiba P (1999) Zur Anwendung von Polyedern und Quadern bei der
Berechnung des Schwerefeldes topographischer Massen, Diplomarbeit,
TU Berlin, Institut für Geodäsie und Geoinformationstechnik.